Nuclear reaction

In nuclear physics and nuclear chemistry, a nuclear reaction is the process in which two nuclei or nuclear particles collide to produce products different from the initial particles. In principle, a reaction can involve more than three particles colliding, but because the probability of three or more nuclei to meet at the same time at the same place is much less than for two nuclei, such an event is exceptionally rare. While the transformation is spontaneous in the case of radioactive decay, it is initiated by a particle in the case of a nuclear reaction. If the particles collide and separate without changing, the process is called an elastic collision rather than a reaction.

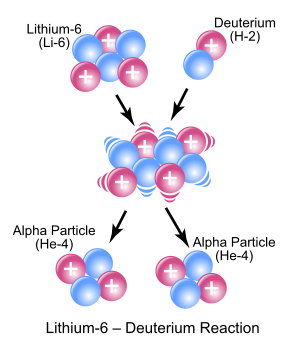
Li6-D Reaction.svg

In the symbolic figure shown to the right, 63Li and deuterium (21H) react to form the highly excited intermediate nucleus 84Be which then decays immediately into two alpha particles. Protons are symbolically represented by red spheres, and neutrons by blue spheres.

63Li  +  21H  →  42He  +  ?

To balance the equation above, the second nucleus to the right must have atomic number 2 and mass number 4; it is therefore also helium-4. The complete equation therefore reads:

63Li  +  21H  →  42He  +  42He

or more simply:

63Li  +  21H  →  2 42He

Contents

Notation

Instead of using the full equations as shown in the previous section, in many situations a compact notation is used to describe nuclear reactions. This is A(b,c)D, which is equivalent to A + b gives c + D. Common light particles are often abbreviated in this shorthand, typically p for proton, n for neutron, d for deuteron, α representing an alpha particle or helium-4, β for beta particle or electron, γ for gamma photon, etc. The reaction above would be written as Li-6(d,α)α.[1][2]

Energy conservation

Kinetic energy may be released during the course of a reaction (exothermic reaction) or kinetic energy may have to be supplied for the reaction to take place (endothermic reaction). This can be calculated by reference to a table of very accurate particle rest masses (see http://physics.nist.gov/PhysRefData/Compositions/index.html), as follows. According to the reference tables, the 63Li nucleus has a relative atomic mass of 6.015 atomic mass units (abbreviated u), the deuterium has 2.014 u, and the helium-4 nucleus has 4.0026 u Thus:

In a nuclear reaction, the total (relativistic) energy is conserved. The "missing" rest mass must therefore reappear as kinetic energy released in the reaction; its source is the nuclear binding energy. Using Einstein's mass-energy equivalence formula E = mc², the amount of energy released can be determined. We first need the energy equivalent of one atomic mass unit:

1 u c² = (1.66054 × 10-27 kg) × (2.99792 × 108 m/s)² 
= 1.49242 × 10-10 kg (m/s)² = 1.49242 × 10-10 J (Joule)
× (1 MeV / 1.60218 × 10-13 J)
= 931.49 MeV,
so 1 u c² = 931.49 MeV.

Hence, the energy released is 0.0238 × 931 MeV = 22.4 MeV.

Expressed differently: the mass is reduced by 0.3 %, corresponding to 0.3 % of 90 PJ/kg is 300 TJ/kg.

This is a large amount of energy for a nuclear reaction; the amount is so high because the binding energy per nucleon of the helium-4 nucleus is unusually high, because the He-4 nucleus is "doubly magic". (The He-4 nucleus is unusually stable and tightly-bound for the same reason that the helium atom is inert: each pair of protons and neutrons in He-4 occupies a filled 1s nuclear orbital in the same way that the pair of electrons in the helium atom occupy a filled 1s electron orbital). Consequently, alpha particles appear frequently on the right hand side of nuclear reactions.

The energy released in a nuclear reaction can appear mainly in one of three ways:

When the product nucleus is metastable, this is indicated by placing an asterisk ("*") next to its atomic number. This energy is eventually released through nuclear decay.

A small amount of energy may also emerge in the form of X-rays. Generally, the product nucleus has a different atomic number, and thus the configuration of its electron shells is wrong. As the electrons rearrange themselves and drop to lower energy levels, internal transition X-rays (X-rays with precisely defined emission lines) may be emitted.

Q-value and energy balance

In writing down the reaction equation, in a way analogous to a chemical equation, one may in addition give the reaction energy on the right side:

Target nucleus + projectile -> Final nucleus + ejectile + Q.

For the particular case discussed above, the reaction energy has already been calculated as Q = 22.4 MeV. Hence:

63Li  +  21H  →  2 42He  +  22.4 MeV

The reaction energy (the "Q-value") is positive for exothermal reactions and negative for endothermal reactions. On the one hand, it is the difference between the sums of kinetic energies on the final side and on the initial side. But on the other hand, it is also the difference between the nuclear rest masses on the initial side and on the final side (in this way, we have calculated the Q-value above).

Reaction rates

If the reaction equation is balanced, that does not mean that the reaction really occurs. The rate at which reactions occur depends on the particle energy, the particle flux and the reaction cross section. An example of a large repository of reaction rates is the REACLIB database, as maintained by the Joint Institute for Nuclear Astrophysics.

Neutrons vs ions

In the initial collision which begins the reaction, the particles must approach closely enough so that the short range strong force can affect them. As most common nuclear particles are positively charged, this means they must overcome considerable electrostatic repulsion before the reaction can begin. Even if the target nucleus is part of a neutral atom, the other particle must penetrate well beyond the electron cloud and closely approach the nucleus, which is positively charged. Thus, such particles must be first accelerated to high energy, for example by:

Also, since the force of repulsion is proportional to the product of the two charges, reactions between heavy nuclei are rarer, and require higher initiating energy, than those between a heavy and light nucleus; while reactions between two light nuclei are the most common ones.

Neutrons, on the other hand, have no electric charge to cause repulsion, and are able to effect a nuclear reaction at very low energies. In fact, at extremely low particle energies (corresponding, say, to thermal equilibrium at room temperature), the neutron's de Broglie wavelength is greatly increased, possibly greatly increasing its capture cross section, at energies close to resonances of the nuclei involved. Thus low energy neutrons may be even more reactive than high energy neutrons.

Notable types

While the number of possible nuclear reactions is immense, there are several types which are more common, or otherwise notable. Some examples include:

Direct reactions

An intermediate energy projectile transfers energy or picks up or loses nucleons to the nucleus in a single quick (10−21 second) event. Energy and momentum transfer are relatively small. These are particularly useful in experimental nuclear physics, because the reaction mechanisms are often simple enough to calculate with sufficient accuracy to probe the structure of the target nucleus.

Inelastic scattering

Only energy and momentum are transferred.

Transfer reactions

Usually at moderately low energy, one or more nucleons are transferred between the projectile and target. These are useful in studying outer shell structure of nuclei.

Reactions with neutrons

→ T → 7Li → 14C
(n,α) 6Li + n → T + α 10B + n → 7Li + α 17O + n → 14C + α 21Ne + n → 18O + α 37Ar + n → 34S + α
(n,p) 3He + n → T + p 7Be + n → 7Li + p 14N + n → 14C + p 22Na + n → 22Ne + p

Reactions with neutrons are important in nuclear reactors and nuclear weapons. While the best known neutron reactions are neutron scattering, neutron capture, and nuclear fission, for some light nuclei (especially odd-odd nuclei) the most probable reaction with a thermal neutron is a transfer reaction:

Some reactions are only possible with fast neutrons:

Compound nuclear reactions

Either a low energy projectile is absorbed or a higher energy particle transfers energy to the nucleus, leaving it with too much energy to be fully bound together. On a time scale of about 10−19 seconds, particles, usually neutrons, are "boiled" off. That is, it remains together until enough energy happens to be concentrated in one neutron to escape the mutual attraction. Charged particles rarely boil off because of the coulomb barrier. The excited quasi-bound nucleus is called a compound nucleus.

See also

Sources

  1. ↑ The Astrophysics Spectator: Hydrogen Fusion Rates in Stars
  2. ↑ http://books.google.com/books?id=ZVgOLCXNoMoC&pg=PA495&lpg=PA495&dq=%22nuclear+reaction%22+parentheses+shorthand&source=web&ots=hVze64yN1C&sig=WQVgiNcZDKFD8nj_i24NInMmGVI&hl=en